Reducers & Leibniz

I found some spare time and decided to explore the new Reducers library in Clojure core, introduced in version 1.5. Clojure is known for its concurrency strengths, but prior to 1.5, it lacked solid built-in support for parallel execution. Since Java 7, it’s been easy to use Fork/Join, but it’s still Java, which lacks the functional abstractions a functional language should provide. Reducers fix this.

Also, a small contest at work was announced: “The most creative approximation of Pi.” I’ve never been nerdy enough to study Pi deeply, but I remembered a method by Gottfried Leibniz from school. After a quick peek in the textbook—Wikipedia—it turned out to be a perfect map-reduce example, fully parallelizable. Since this deals with an approximation of an irrational number, a language supporting rational numbers is a good fit—something many functional languages do well.

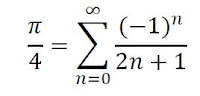
quarter pi

First Attempt: A Naive REPL Translation

(defn exp [x n]
  (reduce *' (repeat n x)))

(defn leibniz [n]
  (/ (exp -1 n) (+' 1 (*' n 2))))

(defn quarter-pi [n]
  (reduce + (map leibniz (range 0 n))))

(time (double (* 4 (quarter-pi 10000))))
;; "Elapsed time: 372310.779121 msecs"
;; => 3.141492653590043

Explanation:

exp calculates x to the power of n using rational-safe multiplication (*').
leibniz returns the nth term in the Leibniz series.
quarter-pi adds up the first n terms.
The result is multiplied by 4 to approximate Pi.

However, it’s slow, and not accurate enough. We need more terms and better performance.

Optimization: Eliminate Power Calculation

Instead of multiplying -1 repeatedly, we use a conditional:

(defn leibniz [n]
  (/ (if (odd? n) -1 1) (+' 1 (*' n 2))))

(time (double (* 4 (quarter-pi 10000))))
;; "Elapsed time: 356521.187414 msecs"
;; => 3.141492653590043

It’s a little faster, but still not great.

Parallel Processing with Reducers

Let’s take advantage of the new Reducers library:

(require '[clojure.core.reducers :as r])

(defn quarter-pi [n]
  (r/fold + (r/map leibniz (vec (range n)))))

(time (double (* 4 (quarter-pi 10000))))
;; "Elapsed time: 1995.426514 msecs"
;; => 3.141492653590043

Observations:

r/map returns a foldable function, not a realized sequence.
r/fold understands how to parallelize the computation.

Huge improvement—almost 200x faster!

Let’s try 100,000 iterations:

(time (double (* 4 (quarter-pi 100000))))
;; "Elapsed time: 90972.733397 msecs"
;; => 3.141582653589793

Comparison:

Math/PI = 3.141592653589793
Our approximation = 3.141582653589793

Not bad.

Rational Madness

Even with just 100,000 terms, the resulting rational has both numerator and denominator in the order of 1.086865e+6! Compare that with Long/MAX_VALUE (~1e+18) or the estimated number of particles in the universe (~1e+80).

Leibniz’s method isn’t efficient but it’s a great example. Apparently, the original form needs 5 billion iterations to reach 10 decimal places.

Final Pretty Version: Parallel Leibniz in Clojure

(defn pi-aprox [n]
  (let [double-up #(*' % 2)
        alter-sign #(if (odd? %) -1 1)
        leibniz #(/ (alter-sign %) (inc (double-up %)))
        natural-numbers (vec (range n))
        reduce clojure.core.reducers/fold
        map clojure.core.reducers/map
        quarter-pi (reduce + (map leibniz natural-numbers))]
    (double (* 4 quarter-pi))))

Let the reduction begin!